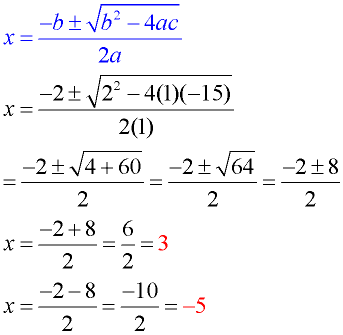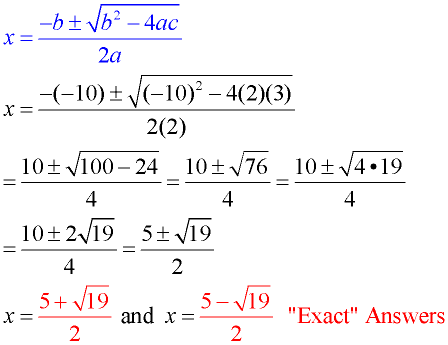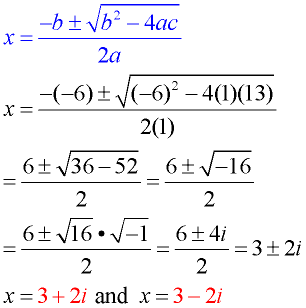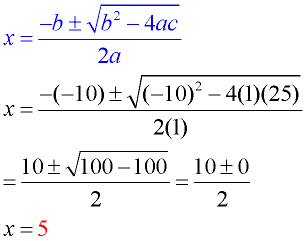|
The solutions for some quadratic equations are not rational, and cannot be obtained by factoring.
The quadratic formula, however, may be used to solve ANY quadratic equation (even the ones that can be factored). This is a formula that you want to know and remember!
 |
•
As you can see in the formula, the coefficients (numbers) "a", "b", and "c" from
ax2 + bx + c = 0 are substituted into the formula.
•
Also notice that the formula will yield two (±) solutions, since a quadratic is a
second degree equation.
• The "2a" in the denominator is underneath the entire top, not just the radical.
• Be careful with the "signs" of the "a", "b", and "c" values in your calculations. |
Let's see the Quadratic Formula at work in various situations:
 Solve: x2 + 2x - 15 = 0 Solve: x2 + 2x - 15 = 0 |
Also factorable. |
Solution using Quadratic Formula: a = 1; b = 2; c = -15
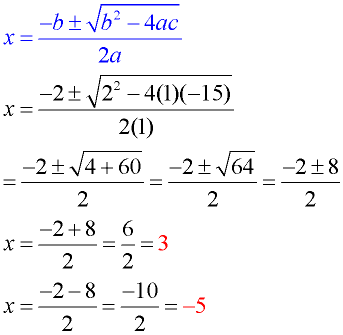
• When the value under the radical is a perfect square, the results will be rational numbers.
|
This equation is also factorable.
(x + 5)(x - 3) = 0
x = -5; x = 3
Notice that the quadratic formula ALSO gives the correct results.
|
 Solve: 2x2 - 10x = -3 Solve: 2x2 - 10x = -3 |
Not set equal to zero! |
Set equation equal to zero: 2x2 -10x + 3 = 0
Solution using Quadratic Formula: a = 2; b = -10; c = 3
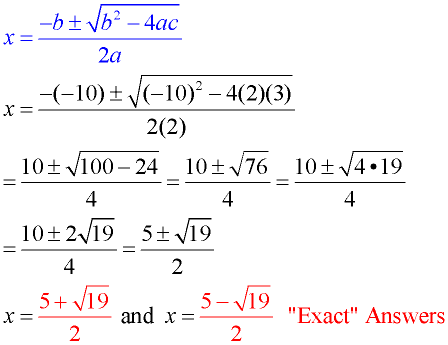

When the value under the radical is not a perfect square (and not negative), the result will be irrational numbers.
|
Not factorable.
Notice the needed parentheses for dealing with the "b" value of "-10".
 Radical answers are"exact" answers.
Radical answers are"exact" answers.
Decimal answers are
"approximate" answers.
|
 Solve: x2 - 6x + 13 = 0 Solve: x2 - 6x + 13 = 0 |
|
Solution using Quadratic Formula: a = 1; b = -6; c = 13
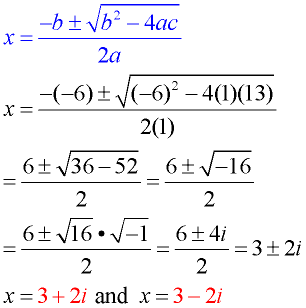
• When the value under the radical is a negative number, the result will be an imaginary number containing i.
|
|
 Solve: x2 -10x + 25 = 0 Solve: x2 -10x + 25 = 0 |
Repeated answer! |
Solution using Quadratic Formula: a = 1; b = -10; c = 25
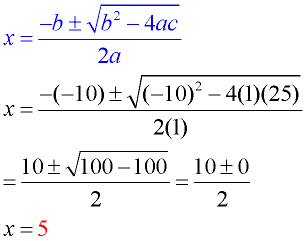
• Be careful here! It appears that there is only ONE answer, but this is actually a "repeated" root.
• The graph is tangent to the x-axis at x = 5.
• When the value under the radical is zero, the result will be one "repeated" root. |
This equation is also factorable.
(x - 5)(x - 5) = 0
x = 5; x = 5
Answer "repeats".
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|