Adding (or subtracting) rational expressions (and other algebraic fractions) requires a
COMMON DENOMINATOR.
You need a common denominator to add numerical fractions,
and you need a common denominator to add algebraic fractions. |
Your teacher may, or may not, ask you to state the domains of rational expressions.
 If you already HAVE a common denominator, life is easier!
| Add or Subtract Rationals that HAVE a Common Denominator: |
To add (or subtract) rational expressions (with a common denominator):
To add (or subtract) rationals with a common denominator:
1. Add or subtract the expressions using the rule stated above.
2. Simplify further if possible. |
Example:
Add: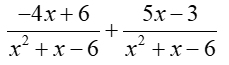
|
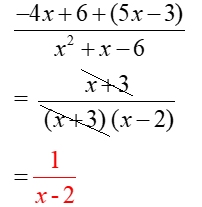
We have a common denominator,
so we go right to adding the numerators.
Factor the denominator.
Cancel (or divide out) the common factor.
Domain: x ≠-3, 2
|
If you DO NOT have a common denominator, more work is needed.
| Add or Subtract Rationals that DO NOT HAVE a Common Denominator: |
You need to find the Least Common Denominator (LCD).
1. Factor each denominator completely.
2. List all of the different factors that appear in the denominators.
3. The LCD is the product of all of the factors in Step 2.
4. Adjust the expressions in the problem to reflect the new LCD.
5. Add or subtract.
4. Simplify further if possible. |
Example 1:
(Use of parentheses.)
Add: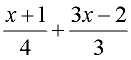 
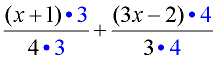
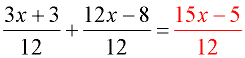
Domain: All real numbers
|
The LCD in this problem is 12.
When adjusting for the LCD, it is necessary to multiply BOTH the numerator and denominator in each fraction by the numerical values of 3, and then 4 respectively to create the LCD of 12.
 The ENTIRE numerator, in each case, must be multiplied, as is shown by the use of parentheses.
Be sure to distribute across the parentheses.
|
| |
Example 2: (Subtracting a quantity.)
Subtract: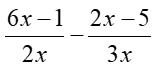 
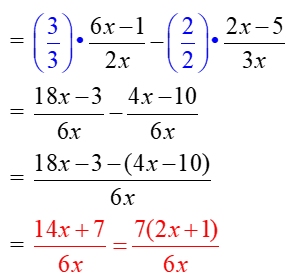Domain: x ≠ 0
|
The LCD for 2x and 3x is 6x.
Adjust each fraction to reflect this new denominator.
A potential "problem spot" in this example is the subtraction of the second numerator. You must subtract the ENTIRE second numerator, not just the first term. Use parentheses around the numerator being subtracted!! When you distribute the negative sign across the parentheses you will be subtracting both terms in the second numerator. |
| |
Example 3: (Factorable denominator.)
Add:
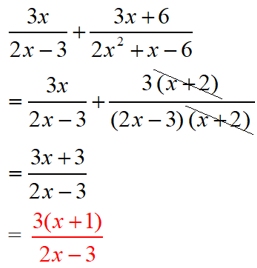
Domain: x ≠ 3/2, -2 |
Both the numertor and the denominator need factoring in this problem.
When factoring a denominator, it may be likely that the denominator of the other expression(s) will be (or contain) one of your newly found factors.
Factoring the second rational expression in this problem proved to be very helpful,
By canceling the factors in the second fraction, it created a common denominator for the problem.
All that was needed then, was to add the numerators. |
| |
Example 4: (Combination problem.)
Add and Subtract: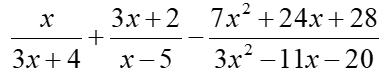
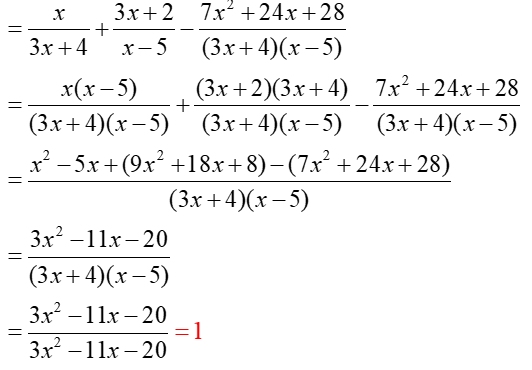
Domain: x ≠
-4/3, 5
When working with multiple expressions, always look to see if the denominators are related to one another in some manner. In this problem the first two denominators were the factors of the third denominator. Nice!
The rest of the problem is just a matter of "careful" calculations. It is not difficult. It is just long.
Be warned ... not all problems of this form will result in an "integer" answer. This answer of "1" is an exception. |
|
