Modifying Rational Expressions - Quotient-Remainder Form

One of the beautiful things about mathematics is the variety of ways to express concepts.
In this lesson, we are going to use the structure of a rational expression to rewrite (modify) the expression to a different form, specifically a "quotient-remainder" form.

There are numerous ways to modify (or rewrite) a rational expression.
Consider these few possible rewrites of a given rational expression: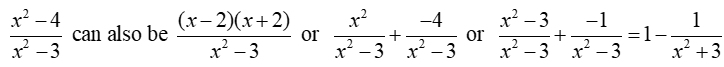

How a rational expression can be modified is based upon the structure and specific features
of the expression. Not all rational expressions contain the same features.

For example, the illustration above shows a rational expression that has the feature of a factorable numerator. But it also has the feature that its numerator can be rewritten to contain the denominator, as seen in the last rewrite. That last rewrite gives us a "quotient-remainder" form.

While "factoring" is usually our first "go to" feature, in this lesson we are going to focus on whether the rational expression possesses the feature where the numerator can be rewritten to contain the denominator. It will be this feature (that we will be examining), which will allow the rational expression to be modified into a "quotient-remainder" form, quickly, without long division.

Methods to obtain a "quotient-remainder" form for a rational expression:

Method 1: Modify by Long Division

When we worked with polynomials, we worked with the Division Algorithm,
which expressed the division of two polynomials as
a quotient plus a remainder divided by the divisor.

By definition, rational expressions are in essence the "division" of two polynomials.

So, rational expressions can also be "modified" into the form stated by the Division Algorithm:

Under long division, we saw results such as

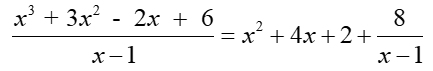
where a rational expression = a quotient + a remainder.

Long division can be applied to a rational expression to produce a "quotient-remainder" form. Keep this in mind if our investigation in Method 2 is not applicable to the given rational.

Method 2: Modify by Inspection

There are certain "simple" rational expressions that have features which allow them
to be modified into a "quotient-remainder" form simply by inspection.
In these expressions, it must be observable (with a little thinking and rearranging) that the numerator can be rewritten into an equivalent form containing the denominator.

Keep in mind that this process will only work for rational expressions whose features
allow for this observable relationship between the numerator and denominator.

If you cannot find such a numerator-denominator relationship,
then long division will be needed to arrive at a "quotient-remainder" form.

Our task, in the following problems,
will be to convert simple rational expressions into the form of a quotient plus a remainder, i.e., . . .

where a and b are integers. by inspection.

Remember that this observable "decomposing" of a rational expression will not work for all rationals.

1. Convert:

The trick is to algebraically separate the denominator out of the numerator and see what is left. It is reverse (or expanded) thinking on how to express the numerator.

2. Convert:

Be sure the adjusted numerator remains equivalent to the original numerator.

3. Convert:

As long as the denominator can be pulled from the numerator, we are up and running.
The numerator can be factored, but factoring will not yield a "quotient-remainder" form.

4. Convert:

This is a little more tricky. Plan ahead, and set up the numerator so that the denominator can be pulled out. 3x + 12 = 3(x + 4). Notice that factoring out the 3 in the numerator will not help us get to a "quotient-remainder" form.

5. Convert:

Showing the parentheses around the denominator in the numerator will help avoid careless mistakes.

6. Show that the following statement is true.
ratsimp26

Notice that the rational has been rewritten in "quotient-remainder" form.

First Answer:

Use the steps in the "inspection" Method 2 to justify this statement as true.
State that the domain must eliminate -2 since it creates a zero denominator in the problem.

Second Answer: Remember that long division will product a "quotient-remainder" form.

By long division, Method 1, it can be seen that the quotient is 1 and the remainder is 1. simprat27

When the remainder is expressed over the divisor, the given statement is shown to be true. The restriction of x ≠ -2 is needed to prevent a zero denominator.
simprat28

7. Rewrite the rational expression ratsimp21

in keeping with ratsimp22

where a(x), b(x), q(x) and r(x) are polynomials and the degree of r(x) is less than the degree of b(x).

ANSWER:
This problem cannot be solved using the simple "inspection" process seen in the examples above, as the relationship between the denominator and numerator is not easily detectable.

This problem is actually asking you to divide the numerator by the denominator, and to write the answer as a quotient with a remainder.

You know how to accomplish this division, but perhaps you have not seen the question asked in this manner.

Note that this expression is undefined for the x-value of -3/2 (as seen by 2x - 3 = 0).

ratsimp23

Are there any benefits to these "quotient-remainder" rewrites?

FAST FORWARD to Graphing Rational Functions

A horizontal asymptote is the line a graph approaches as x → ∞ or x → - ∞.
The asymptote is determined by the ratio of leading coefficients from a single fraction form.

From Example 5 shown above,	In this example, the degrees of the top and bottom are equal and the ratio of leading coefficients is 1/1, or just 1. So, the horizontal asymptote is y = 1. (From process seen when graphing.) The work we did to rewrite this example can actually be used to verify that there is a horizontal asymptote at y = 1.
	Our rewrite clearly points out what is happening when x from this rational is approaching ∞ or - ∞. As the value for x gets extremely large (or small), the denominator of the fraction portion (x² + 8) gets extremely large, making the entire fraction portion 2 / (x² + 8) extremely small, approaching zero.
Thus, the entire statement is approaching 1 + 0, which is 1. This rational function approaches the horizontal line y = 1, verifying our procedure for finding this horizontal asymptote.

As you progress in your study of mathematics, you will see this idea, of expressing a rational expression as the addition of components (including fractions), being developed further. For example, a Calculus process called "Partial Fraction Decomposition" is a rational expression being changed into the sum of a polynomial and one or several fractions with a simpler denominator. Such a rewrite allows for other procedures (that will solve a problem) to be applied to the rewrite, while the former rational expression would not lend itself to a solution.