The goal of simplifying a rational expression is to reduce the expression to its lowest terms. The process is the same as that for simplifying a numerical fraction.
|
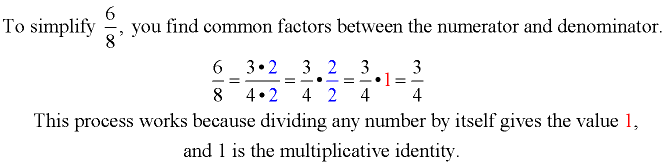(A multiplicative identity when multiplied times a number does not change the number.)
 Steps to Simplifying Rational Expressions: |
1. Factor both numerator and denominator completely.
2. Divide both the numerator and the denominator by any common factors.
3. When needed, state any limitations placed on the domain. |
Simplify:  |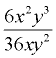
|
This type of rational monomial expression should look familiar
from previous lessons on working with exponents. |
1. If asked, determine the domain of the expression by looking for zero denominator problems.
|
1. Given: 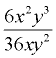Domain: x ≠0, y≠0 |
2. Use your knowledge of working with exponents to simplify this rational expression. |
2. 
|
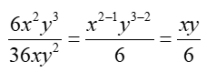
3. Consider the domain of the simplified expression. It appears that it could be "all Reals" since the denominator is never 0. But it is not!
|
3.. The domain of a simplified rational is always stated to be the same
as the domain of the original expression. In this case, the domain remains "all real
numbers, but not x = 0 and not y = 0". |
 Domains of Simplified Rational Expressions:
In the example above, the domain of the simplified expression appears to be "all real numbers",
whereas the domain of the original expression was "all real numbers but not x = 0 nor y = 0."
The domain of the simplified expression is NOT the same as the original domain???
These two expressions are equivalent expressions, which means they have the same values (answers) for all numbers that are in BOTH domains. The numbers in both domains will be the domain of the original expression, which is the more restrictive of the two domains.
When you simplify a rational expression, keep the original domain!
|
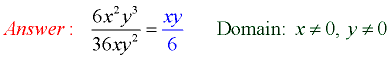
Simplifying with Monomial Terms in Rational Expressions:
Simplify:  |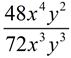
Things to remember:
1. There will be a larger numerical coefficient "remaining" where there was a larger numerical coefficient to "start".
(In this case, the numerical term in the denominator will remain larger than the numerical term in the numerator.)
2. There will be variables
"remaining" where there were larger exponents to "start".
(The exponent of a "remaining" variable is the subtraction (top/bottom) of the exponents of those variables to "start".)
|
Example: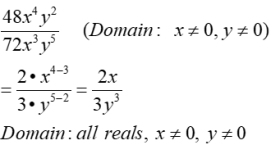
3. The domain is the domain of the original expression.
|
Simplifying with Polynomials in Rational Expressions:
Simplify: 1) 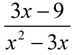 , 2) 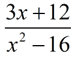 , 3) 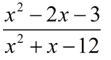 , 4) 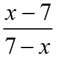 , 5)  |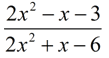
Things to remember:
1. Look for factors first.
2. You cannot reduce "part" of a sum or difference.
3. Reduce "factors", not terms.
(In this example, the entire binomial factor was reduced.)
4. The domain is the domain of the original expression.
|
Example 1: (common factor)
 |
Pay particular attention to  Example 4 above.
The concept of working with (a - b) and (b - a) will appear often.
It is the relationship between these two expressions that is important when factoring.
If either expression is multiplied by "-1", the result contains the other expression.
Given: (a - b)
Multiply by -1: -(a - b) = -a + b
Commute: -a + b = b - a
Result: (b - a)
-(a - b) = (b - a)
- (b - a) = (a - b)
|
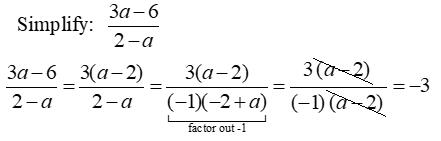
Remember (-2 + a) = (a - 2) by the commutative property. |
|
